LC

题目

谈树的中序遍历

树的中序遍历有2种传统做法，一个是直接递归（利用系统栈），一个是非递归（自己手动开一个栈）。不过，无论哪种方法，都需要用到栈，空间复杂度和树高成正比，最坏情况下为$O(n)$。

LC-94就考了中序遍历。这里贴一个非递归写法，方便以后复习思路。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;

        while(root || stk.size()) {
            while(root) {
                stk.push(root);
                root = root->left;
            }

            if(stk.size()) {
                root = stk.top();
                stk.pop();
                res.push_back(root->val);
                root = root->right;
            }
        }
        return res;
    }
};

为何要用栈

二叉树在中序遍历时，位于上方的点不一定比下方的点先遍历。这个很显然，比如根节点就是在左子树的节点遍历完之后再遍历。但指针是只能向下走的，没有往上走的路，因此我们需要用栈来记录上方待遍历的节点地址。在递归实现中，这叫回溯；在非递归实现中，这叫弹出栈顶元素。

那能不能把这部分空间优化掉呢？

首先考虑什么时候需要回溯。当一个节点的前驱节点不是它的左孩子时，它的前驱节点就需要回溯。而前驱节点在哪？直观上来看，应该是左子树里面中序遍历的最后一个元素，也就是当前节点先向左走一步，然后一直向右走到底的那个位置！

抛开栈，牵线搭桥+过河拆桥

让需要回溯的前驱节点的右孩子链到当前节点，这是Morris算法的核心。这个思路其实很reasonable，因为中序遍历的后继节点的确就是访问当前节点的右子树。通过预先搭桥再遍历的方式，就可以省掉一个栈了。

整体算法流程如下：

  1. 如果当前节点的左孩子为空，那么遍历一下当前节点，然后当前节点更新为右孩子；
  2. 如果当前节点的左孩子不空，那么找到当前节点的前驱节点last
    (1) 如果last的右孩子为空，说明这是第一次到达这里，表示左子树还没被遍历过，那么把last的右孩子更新为当前节点（牵线搭桥），然后当前节点进入左子树遍历；
    (2) 如果last的右孩子不空，说明这是第二次到达这里，表示左子树已经遍历过了，那么把当前节点遍历一下，然后记得把last的右孩子恢复为空（过河拆桥），然后当前节点进入右子树遍历。贴一张原理图，方便日后手动模拟。

LC

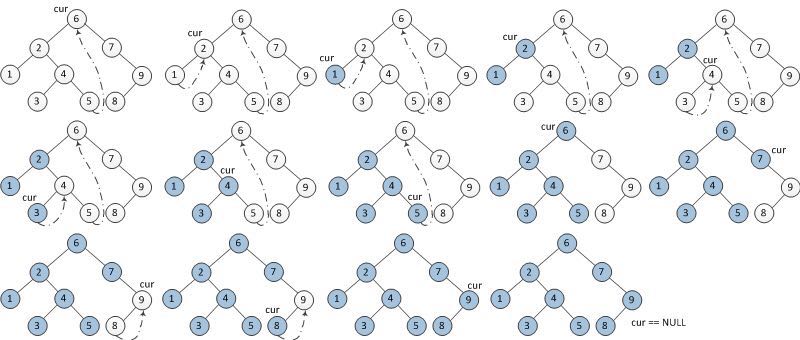
代码

class Solution {
public:
    void recoverTree(TreeNode* root) {
        TreeNode* first = nullptr, *second = nullptr, *last = nullptr;
        while(root) {
            if(root->left) {
                auto p = root->left;
                while(p->right && p->right != root) p = p->right;
                if(p->right) {
                    if(last && last->val >= root->val) {
                        if(!first) first = last, second = root;
                        else second = root;
                    }
                    p->right = nullptr;
                    last = root;
                    root = root->right;
                } else {
                    p->right = root;
                    root = root->left;
                }
            } else {
                if(last && last->val >= root->val) {
                    if(!first) first = last, second = root;
                    else second = root;
                }
                last = root;
                root = root->right;
            }
        }
        swap(first->val, second->val);
    }
};