LC

股票投资系列

总结了3道相关题目：

  1. 买卖股票的最佳时机
  2. 买卖股票的最佳时机 II
  3. 买卖股票的最佳时机 III
  4. 买卖股票的最佳时机 IV
  5. 最佳买卖股票时机含冷冻期

只有一次交易

直观上看，要使得收益最大，在买入时尽量地以低价购入，然后等股票价格最高时卖出即可。注意买入操作需要在卖出操作之前进行。

因此，从左到右依次遍历，维护一个最小值，表示当前时刻之前的股票的最低价格，然后再判断当天卖出是否能得到最大收益即可。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int mini = prices[0], res = 0;
        for(int i = 1; i < prices.size(); i++) {
            mini = min(prices[i], mini);
            res = max(res, prices[i] - mini);
        }
        return res;
    }
};

可以多次交易

在任意时刻，可以随意地卖出和买入，只需保证在买入之前先卖出就行（也就是假设只持有一支股票）。

注意到，如果当天卖出后立刻在当天又买入，其实总收益没有产生变化。比如：

[7, 1, 5, 3, 6, 4]

在第2天买入，在第4天卖出，赚了3 - 1 = 2；

在第2天买入，然后在第三天卖出后立刻买入，然后又在第4天卖出，赚了3 - 5 + 5 - 1 = 2

根据这个性质，可以把所有连续的区间分解成长度为1的区间。问题转换成：给定n - 1个长度为1的区间，选取哪些区间能够让总收益最大？

单个区间的收益很容易计算，右端点$-$左端点就是收益。

因此，总收益最大只需要看一下这些区间中，哪些区间的收益为正就可以了。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res = 0;
        for(int i = 0; i + 1 < prices.size(); i++) {
            res += max(0, prices[i + 1] - prices[i]);
        }
        return res;
    }
};

只能交易2次

求的是2段连续区间，可以考虑利用前后缀分解的做法。

前后缀分解是以第2段区间的左端点作为分割点，把问题分解成左右两端。

举个例子：

[3,3,5,0,0,3,1,4]

以1作为分割点，问题被分解成：

  1. [3,3,5,0,0,3] 交易一次的最大收益
  2. [1, 4] 交易一次的最大收益

那其实就是转换为2个问题一了。

所以，只需要枚举这个分割点，求全部情况的最大值即可。

按照这个思路，枚举分割点需要$O(n)$的时间复杂度，然后求左右两边的最大收益也是需要$O(n)$的复杂度，总的时间是$O(n^2)$的。能不能优化呢？

优化——预处理左区间

在问题一中，我们维护了一个最小值min，不妨设从1~i区间交易1次的最大收益为f[i]，则f[i]可以由2种情况转移（递推）而来。

  1. 当前卖出产生的收益大于最大值，那就调整为在当前时刻卖出，f[i] = prices[i] - min；
  2. 当前卖出产生的收益值小于最大值， 那就不卖，f[i] = f[i - 1]。

于是可以$O(n)$时间预处理出任意时刻的左边区间的最大收益。

优化——预处理右区间

借鉴前面的思路，我们要预处理出i~n区间的最大收益。可以把问题一逆转一下，从后往前遍历（因为问题一求解的是从起点到i的最大收益，而这里正向做的话，起点是变化的，不好处理)。不妨设从i~n区间交易的最大收益为r[i]，维护一个当前时刻右边的最大值，则r[i]也可以从2种情况转移而来：

  1. 当前买入产生的收益大于最大值，那就调整为在当前时刻买入，r[i] = max -prices[i]；
  2. 当前卖入产生的收益值小于最大值， 那就不买，f[i] = f[i + 1]。

于是可以$O(n)$时间预处理出任意时刻的右边区间的最大收益。

最后再遍历一下分割点即可。

总的时间复杂度是: $O(n) + O(n) + O(n) = O(n)$

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<int> f(n + 1);
        for(int i = 1, mini = INT_MAX; i <= n; i++) {
            f[i] = max(f[i - 1], prices[i - 1] - mini);
            mini = min(mini, prices[i - 1]);
        }

        int res = 0;
        for(int i = n, maxi = 0; i; i--) {
            res = max(res, maxi - prices[i - 1] + f[i - 1]);
            maxi = max(maxi, prices[i - 1]);
        }
        return res;
    }
};

只能交易k次

股票系列究极版。

如果$k \ge \lfloor \frac{n}{2} \rfloor$，那么等价于第二题（无限次操作）。因为一次交易需要买入和卖出2次操作，而一天只能进行一次操作，所以最多也就进行$\frac{n}{2} \rfloor$次交易。

对于$k < \lfloor \frac{n}{2} \rfloor$的情况，考虑用状态机DP来解决问题。

首先因为需要保证不能同时参与多笔交易，所以某一天只能有2种状态：手里没有股票、手里持有1支股票。

接下来考虑状态之间是如何转移的，不妨令这两种状态为$f$和$g$。

  • $f \rightarrow g$: 当买入股票时，状态从没有股票转移到有1支股票，此时收益应该减少$w_i$（表示第$i$天股票的价格）
  • $g \rightarrow f$: 当卖出股票时，状态从有1支股票转移到没有股票，此时收益应该增加$w_i$
  • $f \rightarrow f$: 当手里没有股票时，当天不买入
  • $g \rightarrow g$: 当手里有1支股票时，当天不卖出

于是构建出了一个状态机，接下来要在这个状态机上求解买卖股票的最大收益。

将问题转化为适用状态机模型的表达：

已知能走n条边，且最多能转k圈，求所有方案所得收益的最大值

回到DP的集合表示和集合计算。如图所示：

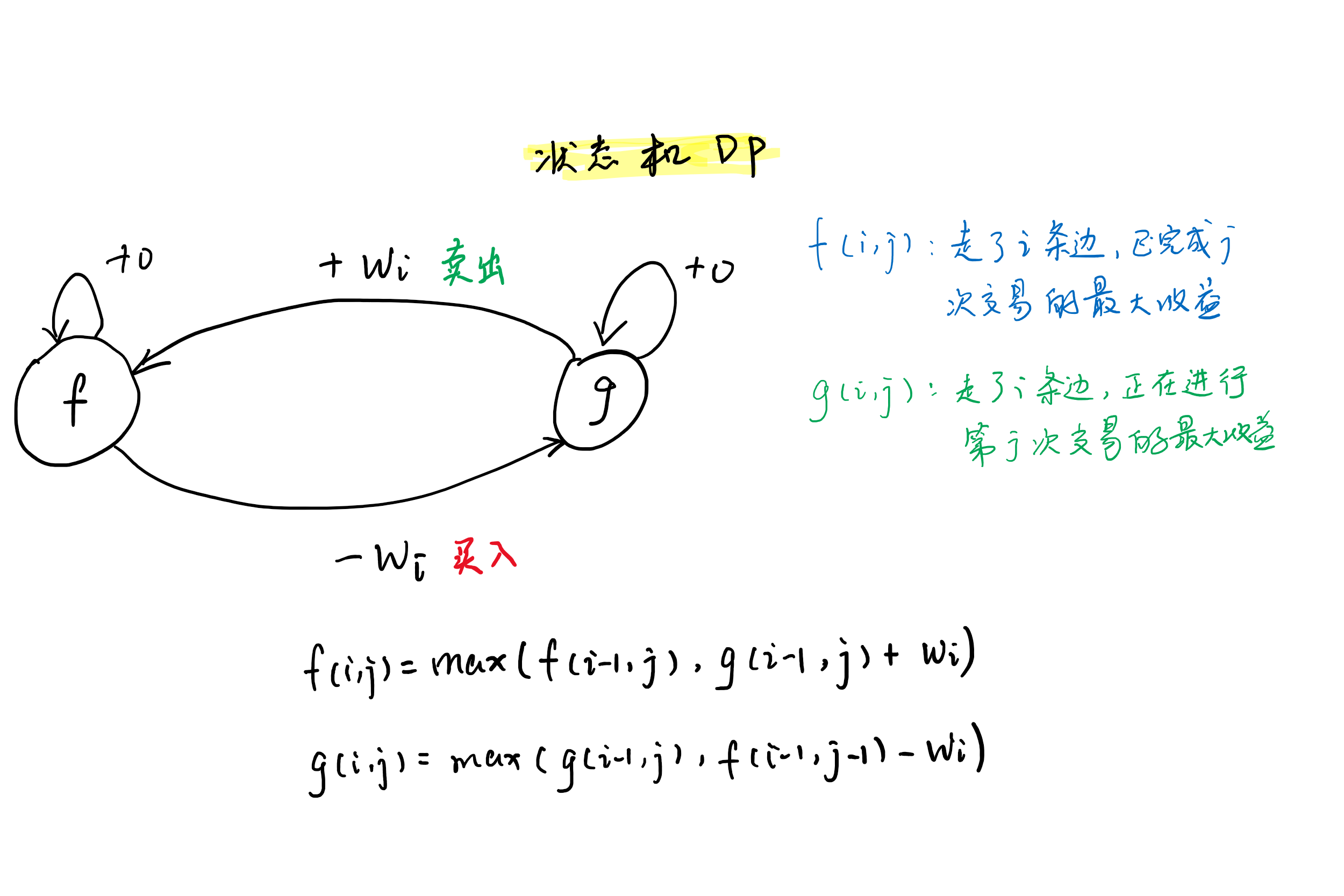
状态机DP

时间复杂度：$O(n^2)$

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        if(k >= n / 2) {
            int res = 0;
            for(int i = 0; i + 1 < n; i++) {
                if(prices[i] < prices[i + 1]) 
                    res += prices[i + 1] - prices[i];
            }
            return res;
        }

        vector<vector<int>> f(n + 1, vector<int>(k + 1, -1e8));
        auto g = f;

        f[0][0] = 0;
        int res = 0;
        for(int i = 1; i <= n; i++) {
            for(int j = 0; j <= k; j++) {
                f[i][j] = max(f[i - 1][j], g[i - 1][j] + prices[i - 1]);
                g[i][j] = g[i - 1][j];
                if(j) g[i][j] = max(g[i][j], f[i - 1][j - 1] - prices[i - 1]);
                res = max(res, f[i][j]);
            }
        }
        return res;
    }
};

含冷冻期

同样是利用状态机DP解决， 一共有3种状态，冷冻期，持有期，卖出期。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> f(n + 1, vector<int>(3, 0));
        f[0][0] = 0, f[0][1] = -prices[0];
        for (int i = 1; i < n; i++) {
            f[i][0] = max(f[i - 1][2], f[i - 1][0]);
            f[i][1] = max(f[i - 1][0] - prices[i], f[i - 1][1]);
            f[i][2] = f[i - 1][1] + prices[i];
        }
        return max(f[n - 1][0], f[n - 1][2]);
    }
};