LC

旋转数组

思路

环形替换

algo1

class Solution {
public:
    int gcd(int a, int b) {
        return b ? gcd(b, a % b) : a;
    }

    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        if(n == 1) return;
        k %= n;
        int count = gcd(k, n);
        for(int i = 0; i < count; i++) {
            int t = nums[i];
            int start = i;
            do{
                i = (k + i) % n;
                swap(t, nums[i]);
            }while(i != start);
        }
    }
};

时间复杂度：因为每个元素只会被操作一次，所以是$O(n)$

翻转法

这个思路比较像脑筋急转弯了。先将整个数组翻转一次，然后前$k$位翻转，后$n-k$位翻转。

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        k %= n;
        rev(nums, 0, n - 1);
        rev(nums, 0, k - 1);
        rev(nums, k, n - 1);
    }

    void rev(vector<int>& nums, int l, int r) {
        while(l < r) {
            swap(nums[l], nums[r]);
            l++;
            r--;
        }
    }
};

时间复杂度：因为每个元素会被操作2次，所以是$O(2n) = O(n)$

补充

这题其实是有背景的Orz… 特地来更新一下

最近在读侯捷的《STL源码剖析》，里面就提到了rotate函数的实现。

为了最大化效率，SGI STL将该函数实现了成几个版本，分别处理不同类型的迭代器：ForwardIterator、BidirectionalIterator、RandomAccessIterator。

roate()进去之后是一个分派函数（dispatch function），观其名知其意，它根据迭代器的型别来分派到不同的函数处理。具体如下：

//dispatch function
template <class ForwardIterator>
inline void rotate(ForwardIterator first, ForwardIterator middle), ForwardIterator last) {
	if (first == last || first == middle) return;
	__rotate(first, middle, last, distance_type(first), iterator_type(first));
}

distance_type()和iterator_type()是两个萃取机，萃取出迭代器的2个特性，从而使得编译器能够根据类型自动匹配到对应的处理函数。

  1. ForwardIterator
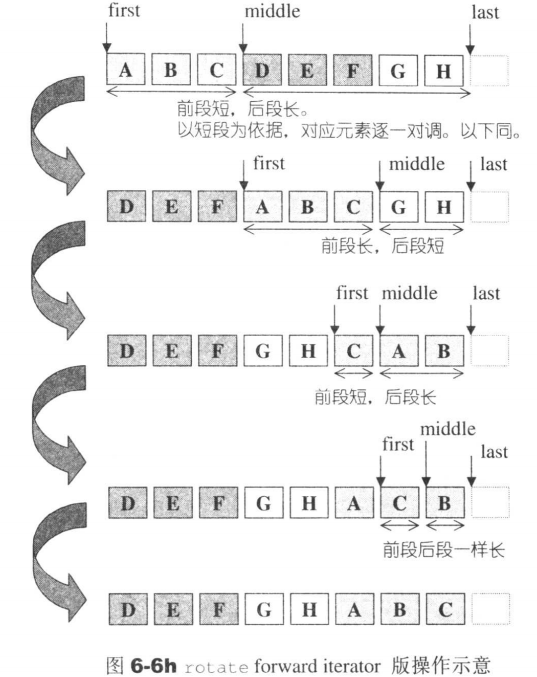
    如果是前向迭代器（即只支持++操作），对应的实现如下：
// SGI STL 源码
template <class ForwardIterator, class Distance>
void __rotate(ForwardIterator first, ForwardIterator middle), ForwardIterator last, Distance*, Forward_iterator_tag) {
	for (ForwardIterator i = middle; ;) {
		iter_swap(first, i); // 前段、后段的元素一一交换
		++first;             // 双双前进1
		++i;
		
		// 以下判断是前端[first, last)先结束还是后段[middle, last)先结束
		if (first == middle) {           // 前段结束了
			if (i == last) return;       // 如果后段同时也结束，整个就结束了
			middle = i;                  // 否则调整，对新的前、后段再作交换
		}
		else if (i == last)         // 后段先结束
			i = middle              // 调整，准备对新的前、后段再作交换
	}
}
  1. BidirectionalIterator
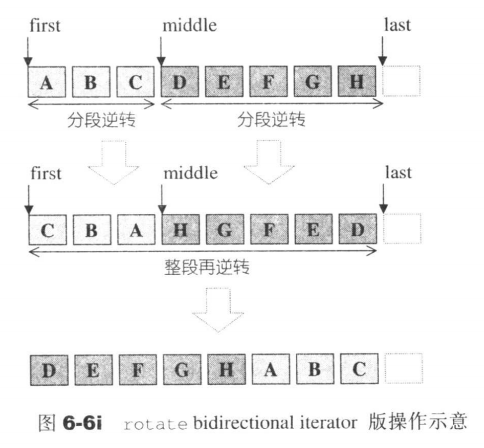
    如果是双向迭代器（同时支持++和--操作），对应的实现如下：

刚好就是上面的翻转法！！

template <class BidirectionalIterator, class Distance>
void __rotate(BidirectionalIterator first, BidirectionalIterator middle), BidirectionalIterator last, Distance*, bidirectional_iterator_tag) {
	reverse(first, middle);
	reverse(middle, last);
	reverse(first, last);
}
  1. RandomAccessIterator
    如果是随机访问迭代器（同时支持++,--还有+n、-n操作），对应的实现如下：

刚好就是上面的环形替换法！！

template <class RandomAccessIterator, class Distance>
void __rotate(RandomAccessIterator first, RandomAccessIterator middle), RandomAccessIterator last, Distance*, random_access_iterator_tag) {
	Distance n = __gcd(last - first, middle - first);
	while (n--) {
	__rotate_cycle(first, last, first + n, middle - first, value_type(first));
	}
}

template <class RandomAccessIterator, class Distance, class T>
void __rotate_cycle(RandomAccessIterator first, RandomAccessIterator last), RandomAccessIterator initial, Distance shift, T*) {
	T value = *initial;                               // 存一下起始位置的值
	RandomAccessIterator ptr1 = initial;
	RandomAccessIterator ptr2 = ptr1 + shift;         // 向后跨一定的步长
	while (ptr2 != initial) {
		*ptr1 = *ptr2;                                // 向前挪动
		ptr1 = ptr2;
		if (last - ptr2 > shift)                      // 判断是否到达了尾端
			ptr2 += shift;
		else 
			ptr2 = first + (shift - (last - ptr2));
	}
	*ptr1 = value;
}

个人观点: STL的实现还不如LC题解的实现，因为while中间还多了一重if else，或许效率上比较慢？取模不是更直接？

前两种的图解（source from 《STL 源码剖析》)

STL1

STL2