LC

题目

哪种连续子字符串更长
准时到达的列车最小时速
跳跃游戏 VII
石子游戏 VIII

题解

第一题是一个简单的模拟题，直接根据题意模拟即可。

Code Q1

class Solution {
public:
    bool checkZeroOnes(string s) {
        int one = 0, zero = 0;
        for(int i = 0; i < s.size(); i++) {
            int j = i;
            char t = s[j];
            while(j < s.size() && s[j] == t) j++;
            if(t == '0') {
                int diff = j == i ? 1 : j - i;
                zero = max(zero, diff);
            }
            else {
                int diff = j == i ? 1 : j - i;
                one = max(one, diff);
            }
            i = j - 1;
        }
        return one > zero;
    }
};

第二题是一个二分题，每当时速确定时，总可以对应唯一一个总时间；并且时速越大，时间越短（严谨来说是非递增），所以问题具有二段性，可以用二分来做。

注意这里用到一个小技巧：如何求$\lceil \frac{a}{b} \rceil$?
答案是利用公式：$\lceil \frac{a}{b} \rceil = \lfloor \frac{a + b - 1}{b} \rfloor$

Code Q2

class Solution {
public:
    
    vector<int> d;
    
    double check(int x) {
        double res = 0;
        for(int i = 0; i < d.size() - 1; i++) {
            res += (d[i] + x - 1) / x;
        }
        res += d[d.size() - 1] * 1.0 / (x * 1.0);
        return res;
    }
    
    int minSpeedOnTime(vector<int>& dist, double hour) {
        d = dist;
        int l = 1, r = 1e7 + 1;
        while(l < r) {
            int mid = l + r >> 1;
            if(check(mid) <= hour) r = mid;
            else l = mid + 1;
        }
        return l == 1e7 + 1 ? -1 : l;
    }
};

第三题考试时没想出来，主要是一开始就没往DP的方向去想。。

直接上图：

Q3

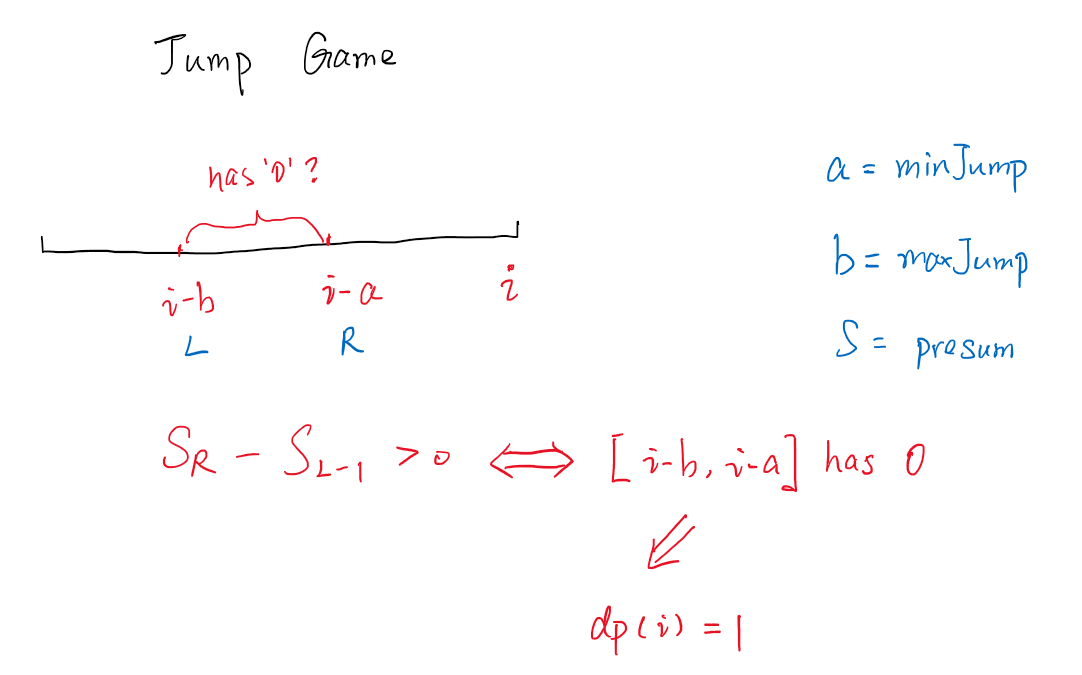
其中的前缀和优化dp算是一个经典模型，这里是求部分和时可以把$O(n)$优化到$O(1)$。类似地，如果求滑动窗口的最值，可以利用单调队列优化；如果求任意区间的最值，可以利用线段树。

Code Q3

class Solution {
public:
    bool canReach(string str, int a, int b) {
        int n = str.size();
        vector<int> s(n + 1), f(n + 1);
        str = ' ' + str;
        f[1] = 1;
        s[1] = 1;
        for(int i = 2; i <= n; i++) {
            if (str[i] == '0' && i - a > 0) {
                int l = max(1, i - b), r = i - a;
                if (s[r] - s[l - 1] > 0) f[i] = 1;
            }
            s[i] = s[i - 1] + f[i];
        }
        return f[n];
    }
};

这里再贴一个BFS做法，BFS思路比较直接，就是将队列头所有能跳到的合法点都入队，但是需要剪枝，这个剪枝的正确性是不直观的，需要稍微证明一下。

class Solution {
public:
    int dp[100010]={0};
    bool canReach(string s, int minJump, int maxJump) {
        dp[0]= 1;
        queue<int> q;
        q.push(0);
        while(!q.empty()){
            int idx = q.front(); q.pop();
            if(idx >=s.size()-1) return true;
            for(int i = idx+minJump;i<= idx+maxJump;i++){
                if(i >= s.size()) break;
                if(s[i]=='0' && dp[i]==0){
                    q.push(i); dp[i] =1;
                }else if(s[i]=='0' && dp[i] ==1){
                	// 关键剪枝。这里为什么可以break？因为后面的合法点都会被队列中存的后续点所遍历到，因此后面的部分是多余的。
                    break;
                }
            }
        }

        return false;
    }
};

第四题和第三题的做法有些相似，但是背景完全不同。第四题是一个一般的博弈论问题，即要求最坏情况下最好的结果（博弈论的精髓所在，将对手视为足够聪明的人，每一步博弈都站在对手做出最优选择的情况（也就是我方最劣情况）下来决策）。

Q4

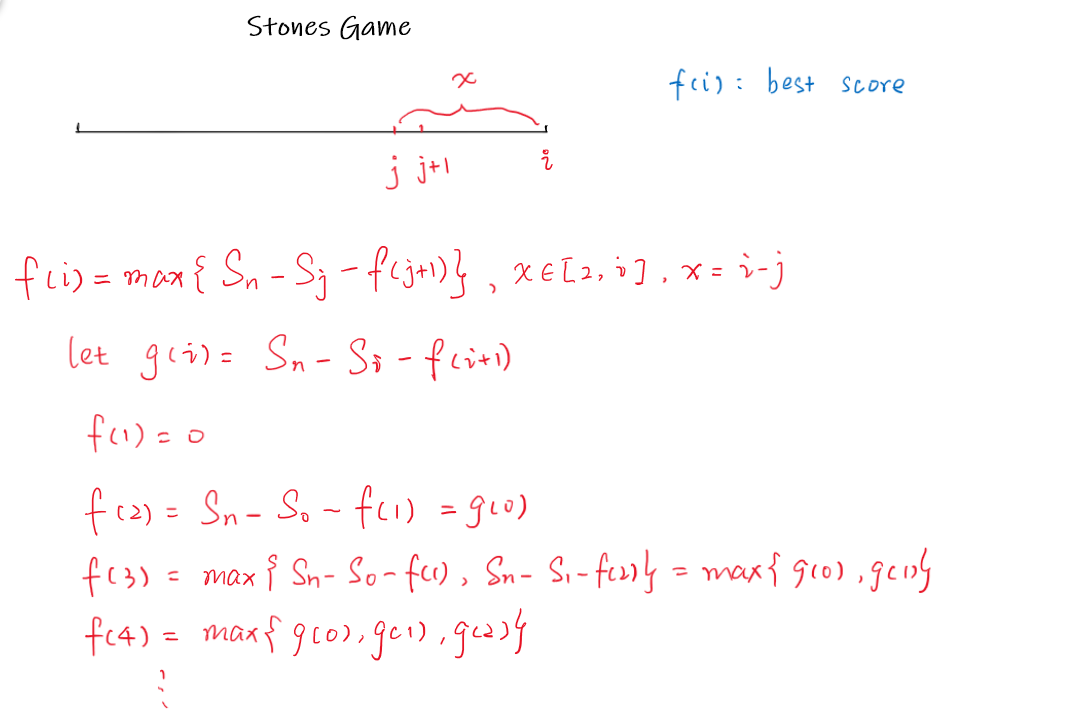
根据递推式，状态数是$O(n)$的，状态转移也需要$O(n)$，所以总的时间复杂度是$O(n^2)$级别，看一眼数据范围$10^5$，会超时。因此考虑优化，注意到每次计算f[i]时其实用到的是前面g[0]~g[i-1]的最大值，因此可以用一个变量维护g的前缀最大值，这样就不用每次都从g[0]开始算了，少了一重循环。

Code Q4

class Solution {
public:
    int stoneGameVIII(vector<int>& stones) {
        int n = stones.size();
        reverse(stones.begin(), stones.end());
        vector<int> f(n + 1), s(n + 1);
        for(int i = 1; i <= n; i++) s[i] = s[i - 1] + stones[i - 1];
        int v = s[n] - s[0] - f[1];
        for(int i = 2; i <= n; i++) {
            f[i] = v;
            v = max(v, s[n] - s[i - 1] - f[i]);
        }
        return f[n];
    }
};