LC

题目

长度为三且各字符不同的子字符串
数组中最大数对和的最小值
矩阵中最大的三个菱形和
两个数组最小的异或值之和

题解

第一题直接暴力枚举即可。

Code Q1

class Solution {
public:
    unordered_set<string> S;
    
    int countGoodSubstrings(string s) {
        int res = 0;
        if (s.size() < 3) return res;
        for(int i = 0; i < s.size() - 2; i++) {
            string t = s.substr(i, 3);
            if (t[0] != t[1] && t[0] != t[2] && t[1] != t[2])
                res ++;
        }
        return res;
    }
};

第二题要使得最大数对的和最小，也就是要让两个加数尽可能小。探测具有贪心性质，也就是把数组排序后，首位两个数俩俩配对即为最优解。证明如下：

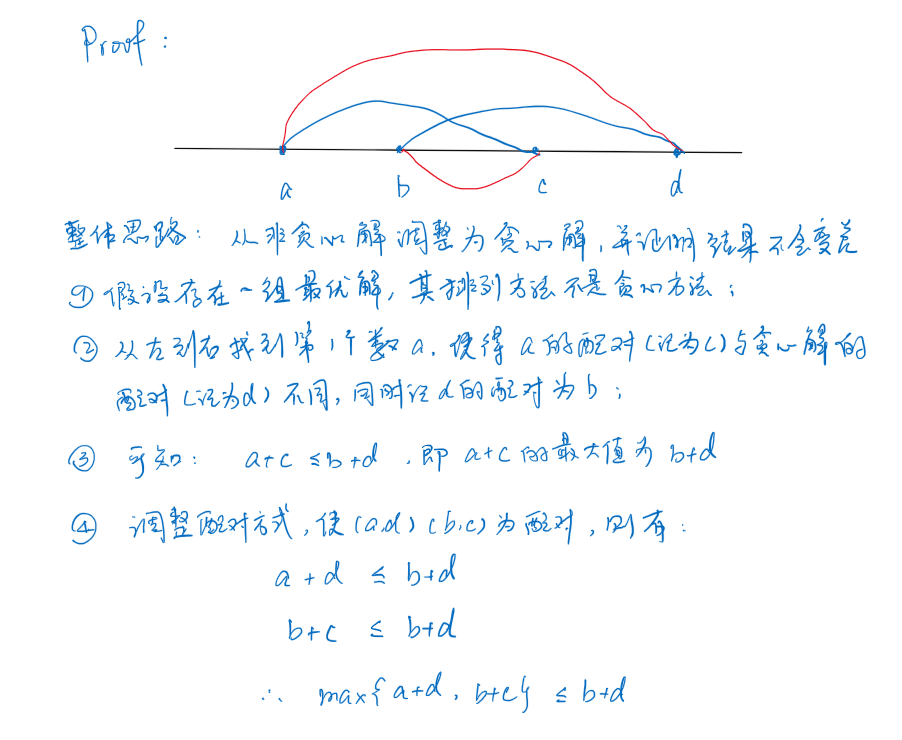
proof

Code Q2

class Solution {
public:
    int minPairSum(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int res = 0;
        for(int i = 0, j = nums.size() - 1; i < j; i++, j--) {
            res = max(res, nums[i] + nums[j]);
        }
        return res;
    }
};

第三题可以按照菱形的边长来枚举所有合法（在矩形内的）菱形，因为边长最大也只有100，所以$O(n^3)$是可以的。

Code Q3

class Solution {
public:
    set<int> S;
    vector<vector<int>> g;
    int dx[4] = {1, 1, -1, -1}, dy[4] = {1, -1, -1, 1};
    
    int cal(int x, int y, int len) {
        int res = 0;
        if (len == 0) return g[x][y];
        int a = x, b = y;
        for(int d = 0; d < 4; d++) {
            for(int i = 0; i < len; i++) {
                a += dx[d], b += dy[d];
                res += g[a][b];
            }
        }
        return res;
    }
    
    
    vector<int> getBiggestThree(vector<vector<int>>& grid) {
        g = grid;
        int n = grid.size(), m = grid[0].size();
        int L = min(n, m);
        for(int len = 0; len <= L / 2; len++) {
            for(int i = 0; i < n - 2 * len; i++) {
                for(int j = len; j < m - len; j++) {
                    S.insert(cal(i, j, len));
                }
            }
        }
        auto it = --S.end();
        int first = *it;
        if (it == S.begin()) return {first};
        it --;
        int second = *it;
        if (it == S.begin()) return {first, second};
        it --;
        int third = *it;
        if (it == S.begin()) return {first, second, third};
        return {first, second, third};
    }
};

第四题是一个状压DP题，这类题型感觉还不是很熟手，虽然结束后看代码就秒懂了，但是自己推还是会出现一些问题，这里好好反思一下。

首先看到数据范围$n \le 14$可以知道本题的解法为暴力枚举或者状态压缩。但是计算一下$14!$发现妥妥的TLE，所以不能直接去枚举所有排列。

注意到，对于下标为 $i$的位置，我们其实不关心 $i$之前的数是怎么排列的（即不考虑顺序），只关心哪些数被用过了（这些数被放在 $i$的前面）。为什么关心这个？因为这决定了当前位置能够用哪些数（因为每个数只能用一次，用过了就不能再用了）。

所以可以用f[s]来表示状态为s时的答案。其中s视为一个二进制数。举个例子：
假设一共有6个数字，
f[100001]表示第1个和最后一个数字已经被选，这2个数被调整为第1和第2个位置。

如何递推？

因为s是从小到大枚举的，所以我们要枚举所有被选过的位置，然后把该位置的数标为不选（这时候的状态一定是小于s的），此时的状态必然是之前计算过的，可以直接拿来用。把所有状态取个min就是我们当前状态的答案。举个例子：

f[100001] = min(f[000001] + (nums1[1] ^ nums2[0]),
                 f[100000] + (nums1[1] ^ nums2[5]))

最后的答案应该是所有的数都被选过的状态对应的数，即f[(1 << n) - 1]

Code Q4

class Solution {
public:
    int minimumXORSum(vector<int>& nums1, vector<int>& nums2) {
        int n = nums1.size();
        vector<int> f(1 << n, 1e9);
        f[0] = 0;
        for(int i = 0; i < 1 << n; i++) {
            int s = 0;
            for(int j = 0; j < n; j++)
                if (i >> j & 1) s++;
            for(int j = 0; j < n; j++) {
                if (i >> j & 1) {
                    f[i] = min(f[i], f[i - (1 << j)] + (nums1[s - 1] ^ nums2[j]));
                }
            }
        }
        return f[(1 << n) - 1];
    }
};