LC

反思

这场周赛可以说是有史以来做得最不顺手的一次了T_T，前期雪崩的开局，第一题直接WA了5发。这次的第一题比较像思维题，一开始没想到要往整除哪方面去想，结果面向数据编程了……第二题看出是二分啪啪啪就开始码题了，结果LC评测机居然卡了unordered_set…….过了66/66个数据显示超时，原地怀疑人生，虽然感觉有可能是set那边的问题，但是还是跳到第三题。此时已经剩下半小时了，一看第三题有1000+通过，应该比第二题简单（想到这又嘀咕着血亏了这波）。匆忙看第三题，一看数据范围感觉就是贪心，匆忙之中WA了一发最后过了。最后剩下10分钟左右回来看第二题，此时靠直觉觉得unordered_set的插入应该是瓶颈，果断换成数组标记的方式，最后提交AC了。长舒一口气，本以为这场要2题收尾，好在最后还是把会做的题都过了。不过罚时就相当难看了，还是不够稳吧，也跟这段时间没常规性刷题有关。比赛遇到码量稍高的题就写得龟速，感觉还是不够熟练吧。

题解

重新分配字符使所有字符串都相等

这个题其实是有些智力题的感觉。可以一开始把全部的字符都挪到一个位置，然后重新分配这些字符。要使得全部的单词相等，那么必须每种字符的数量都能够被$n$整除，$n$是数组长度。

Code Q1
class Solution {
public:
    bool makeEqual(vector<string>& words) {
        int n = words.size();
        unordered_map<char, int> hash;
        for(auto word : words) {
            for(char c : word) {
                hash[c] ++;
            }
        }
        for(auto [c, s] : hash) {
            if (s % n) return false;
        }
        return true;
    }
};

可移除字符的最大数目

这个题考察二分搜索。因为最终的答案$k$满足二段性，即取比$k$小的值时，$p$一定是$s$的子序列，而取比$k$大的值时，反之。因此可以对$k$进行二分，每次需要判断去除若干字符后，$p$是否为$s$的子序列，这个可以用双指针来写。

总时间为$O(nlogn)$

Code Q2
class Solution {
public:
    vector<int> A;
    string s;
    string p;

    bool check(int mid) {
        vector<bool> f(1e5 + 2, 0);
        for(int i = 0; i <= mid; i++) f[A[i]] = true;

        int j = 0;
        for(int i = 0; i < s.size(); i++) {
            if (f[i]) continue;
            
            while (j < p.size() && s[i] == p[j]) {
                i++, j++;
                if (f[i]) break;
            }
        }
        return j == p.size();
    }

    int maximumRemovals(string _s, string _p, vector<int>& removable) {
        int n = removable.size();
        A = removable;
        s = _s; p = _p;
        int l = -1, r = n - 1;
        while(l < r) {
            int mid = l + r + 1 >> 1;
            if (check(mid)) l = mid;
            else r = mid - 1;
        }
        return l + 1;
    }
};

合并若干三元组以形成目标三元组

如果要构成目标三元组，那么不能选某个位置比目标对应位置大的元素，按照这个准则遍历一下数组即可。

Code Q3
class Solution {
public:
    bool mergeTriplets(vector<vector<int>>& triplets, vector<int>& target) {
        vector<int> res = {-1, -1, -1};
        for (auto t : triplets) {
            if (t[0] <= target[0] && t[1] <= target[1] && t[2] <= target[2]) {
                res[0] = max(t[0] ,res[0]);
                res[1] = max(t[1], res[1]);
                res[2] = max(t[2], res[2]);
            }
        }
        if (res[0] == -1) return false;
        return res == target;
    }
};

最佳运动员的比拼回合

万年做不出的第四题，这次的T4还巨恶心，大佬们都得搞一个小时。。。

赛后复盘也琢磨了许久，总算理清楚这几个case了。

1
2
3
4
5
6

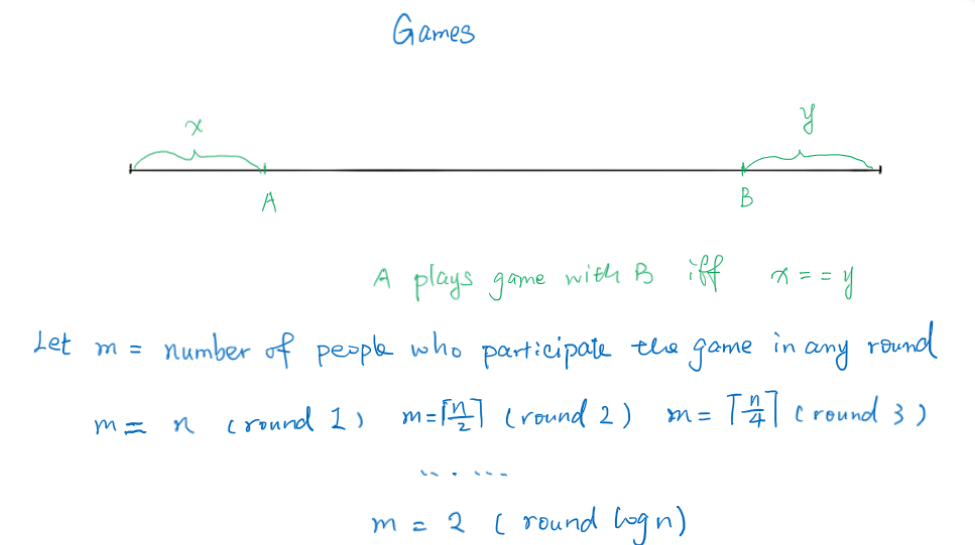
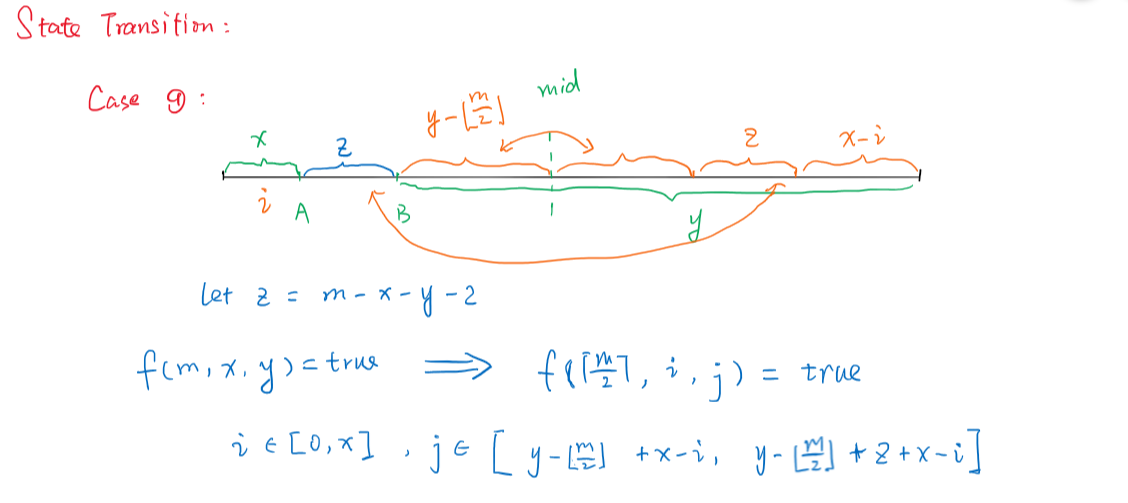
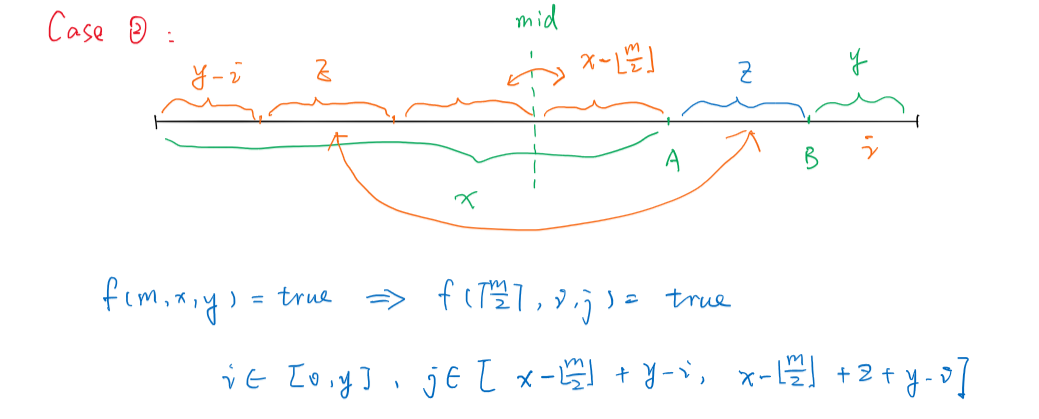
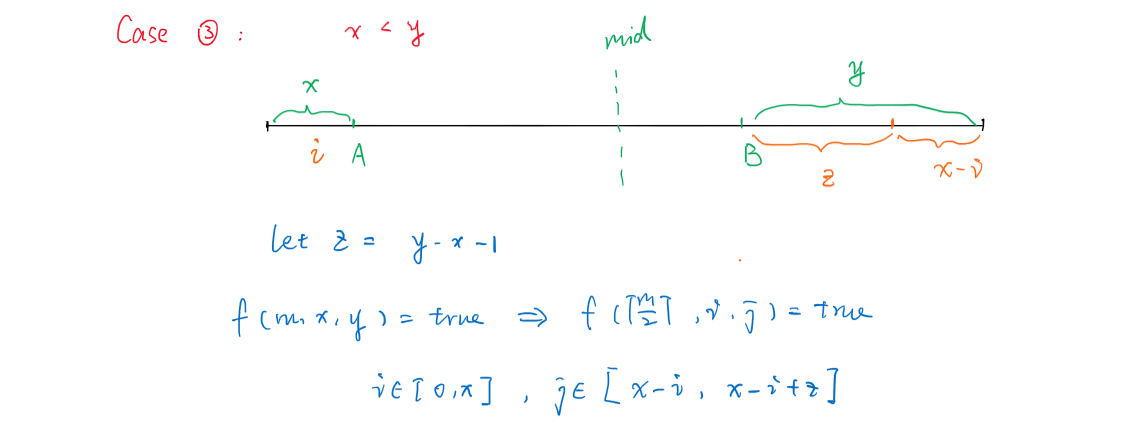
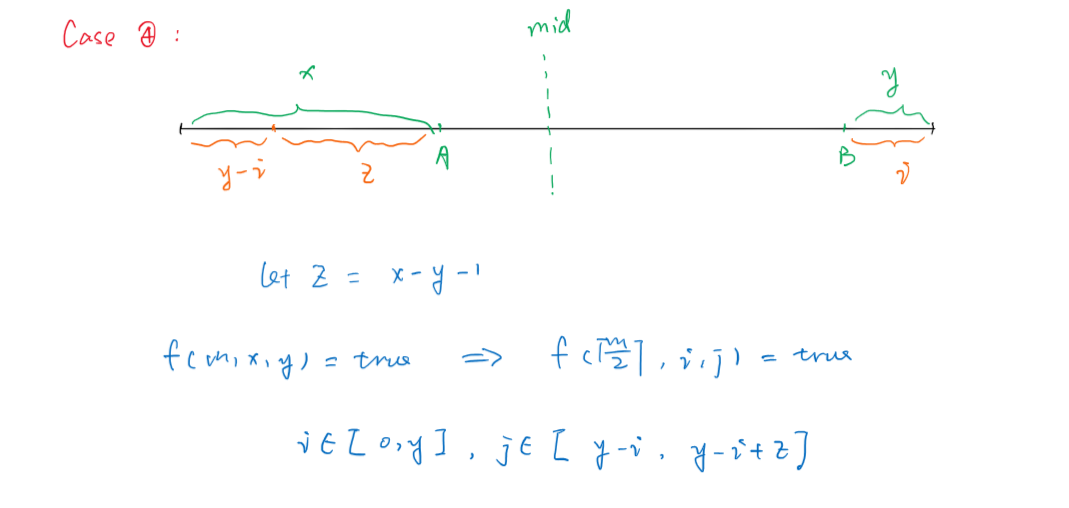
时间复杂度：$O(n^4logn)$

Code Q4

const int N = 30;

int f[N][N][N];

class Solution {
public:
    vector<int> earliestAndLatest(int n, int a, int b) {
        memset(f, 0, sizeof f);
        f[n][a - 1][n - b] = 1;
        for(int m = n; m > 1; m = (m + 1) / 2) 
            for(int x = 0; x <= n; x++) 
                for(int y = 0; y <= n; y++) 
                    if (f[m][x][y]) {
                        int u = (m + 1) / 2;
                        if (y >= m - u) {
                            int z = m - x - y - 2;
                            for(int i = 0; i <= x; i++)
                                for(int j = 0; j <= z; j++)
                                    f[u][i][y - m + u + j + x - i] = 1;
                        } else if (x >= m - u) {
                            int z = m - x - y - 2;
                            for(int i = 0; i <= y; i++) 
                                for(int j = 0; j <= z; j++)
                                    f[u][x - m + u + j + y - i][i] = 1;
                        } else if (x < y) {
                            int z = y - x - 1;
                            for(int i = 0; i <= x; i++)
                                for(int j = 0; j <= z; j++) 
                                    f[u][i][j + x - i] = 1;
                        } else if (x > y) {
                            int z = x - y - 1;
                            for(int i = 0; i <= y; i++)
                                for(int j = 0; j <= z; j++)
                                    f[u][j + y - i][i] = 1;
                        }
                    }
        
        int r1 = INT_MAX, r2 = INT_MIN;
        for(int m = n, t = 1; m > 1; m = (m + 1) / 2, t++) 
            for(int x = 0; x <= n; x++) {
                if (f[m][x][x]) {
                    r1 = min(r1, t);
                    r2 = max(r2, t);
                }
            }
        return {r1, r2};
        
    }
};