LC

反思

Dijkstra太久没写卡了半天T3，回去罚抄10遍

题解

使用特殊打字机键入单词的最少时间

稍微有点麻烦的模拟，要使得总时间最少，可以看成次 转+键入 的时间最少，键入的时间是固定的，所以每次要转最少步数。因此只需要判断顺时针和逆时针旋转哪一个更少步数即可。

Code Q1
class Solution {
public:
    int minTimeToType(string word) {
        char cur = 'a';
        int res = 0;
        for (char c : word) {
            res += min(abs(cur - c), 26 - abs(cur - c)) + 1;
            cur = c;
        }
        return res;
    }
};

最大方阵和

找规律题。可以观察出几个规律：

  1. 当场上只有唯一负数时，负号可以经过取反操作移动到全图的任意位置。具体地，某一个负数周围是正数，取反操作后，符号转移到相邻的数上，因为横竖都可以操作，所以该符号可以全图移动；
  2. 当场上负数个数为偶数时，总可以消掉全部负号。首先将所有相邻的负数全都取反操作成正数，剩下的非相邻负数，可以通过1的方式操作到一起（相邻），然后再取反抵消负号；
  3. 当场上负数个数为奇数个时，总可以操作成一个负数，原理同上。

因此问题转换成：

  1. 若负数个数为奇数，找出全图的最小值，并将其从全图剩余数的正数和中减去；
  2. 若负数个数为偶数，则返回全图正数和。
Code Q2
class Solution {
public:
    long long maxMatrixSum(vector<vector<int>>& f) {
        long long res = 0;
        int n = f.size(), m = f[0].size();
        
        int cnt = 0;
        int mm = INT_MAX;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (f[i][j] < 0) {
                    cnt ++;
                    res += -f[i][j];
                    mm = min(mm, -f[i][j]);
                } else {
                    res += f[i][j];
                    mm = min(mm, f[i][j]);
                }
            }
        }
        
        if (cnt % 2 == 0) return res;
        return res - mm - mm;
    }
};

到达目的地的方案数

可以先求出每个点到原点的最短距离（利用最短路算法）；利用最短路将原图改为一个DAG，然后再做一个计数DP，具体地，设f[i]表示从原点到结点i的所有最短路径数，转移方程为：$f[i] = \sum_k f[k], (k, i)$ $\text{is an edge of shortest path}$

Code Q3
using LL = long long;
const int MOD = 1e9 + 7;
const LL INF = 1e18;
typedef pair<int, int> PII;

class Solution {
public:
    vector<vector<LL>> map;
    vector<LL> dist;
    vector<bool> st;
    vector<int> f;

    void dijkstra() {
        int n = map.size();
        dist = vector<LL>(n, INF);
        st = vector<bool>(n, false);
        priority_queue<PII, vector<PII>, greater<PII>> q;
        q.push({0, 0});
        dist[0] = 0;
        while (q.size()) {
            auto t = q.top();
            q.pop();
            int d = t.first, u = t.second;
            
            if (st[u]) continue;
            st[u] = true;

            for (int i = 0; i < n; i++)
                if (map[u][i] < INF && dist[u] + map[u][i] < dist[i]) {
                    dist[i] = dist[u] + map[u][i]; 
                    q.push({dist[i], i});
                }   
        }
    }

    int dfs(int u, vector<vector<LL>> &g) {
        if (u + 1 == map.size()) return 1;
        if (f[u] != -1) return f[u];
        f[u] = 0;
        for (int i = 0; i < g.size(); i++) {
            if (g[u][i] < INF)
                f[u] = ((LL)f[u] + dfs(i, g)) % MOD;
        }
        return f[u];
    }

    int countPaths(int n, vector<vector<int>>& roads) {
        map = vector<vector<LL>>(n, vector<LL>(n, INF));
        for (auto v : roads) {
            int a = v[0], b = v[1], c = v[2];
            map[a][b] = map[b][a] = c;
        }
        

        dijkstra();

        vector<vector<LL>> g = vector<vector<LL>>(n, vector<LL>(n, INF));
        for (int i = 0; i < n; i++) 
            for (int j = 0; j < n; j++) 
                if (map[i][j] < 1e18) 
                    if (dist[i] - dist[j] == map[i][j]) g[j][i] = map[i][j];

        st = vector<bool>(n, false);
        f = vector<int>(n, -1);
        return dfs(0, g);

    }
};

划分数字的方案数

字符串DP，朴素做法需要$O(n^3)$，枚举状态是$O(n^2)$，状态转移需要$O(n)$。可以利用前缀和（类似于完全背包的优化思路） + 最长公共前缀两个预处理来把转移过程降到常数。

详情见下图：
T4
T4-1
T4-2

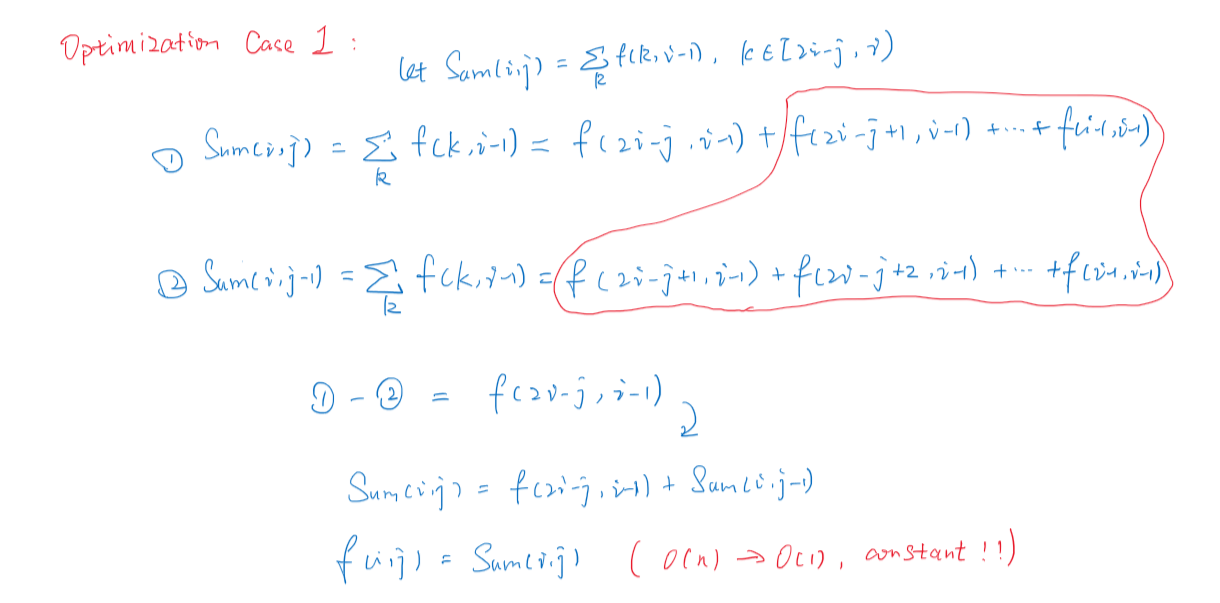
Code Q4
using LL = long long;
const int MOD = 1e9 + 7;
class Solution {
public:
    vector<vector<int>> lcp;
    vector<vector<int>> f;
    string s;

    bool check(int k, int i, int j) {
        int len = lcp[k][i];
        return len >= j - i + 1 || s[k + len] < s[i + len];
    }

    int numberOfCombinations(string num) {
        if (num[0] == '0') return 0;
        int n = num.size();
        s = num;
        lcp = vector<vector<int>>(n + 1, vector<int>(n + 1, 0));
        f = vector<vector<int>>(n + 1, vector<int>(n + 1, 0));

        for (int i = n - 1; i >= 0; i--) 
            for (int j = n - 1; j >= 0; j--) 
                if (s[i] == s[j])
                    lcp[i][j] = lcp[i + 1][j + 1] + 1;

        for (int i = 0; i < n; i++) f[0][i] = 1;
        for (int i = 1; i < n; i++) {
            if (s[i] == '0') continue;
            for (int j = i, k = i - 1, sum = 0; j < n; j++, k--) {
                f[i][j] = sum;
                if (k < 0) continue;
                if (s[k] > '0' && check(k, i, j)) f[i][j] = ((LL)f[i][j] + f[k][i - 1]) % MOD;
                sum = ((LL)sum + f[k][i - 1]) % MOD;
            }
        }

        int res = 0;
        for (int i = 0; i < n; i++) 
            res = ((LL)res + f[i][n - 1]) % MOD;

        return res;
        
    }
};