LC

Solution

使数组按非递减顺序排列

思路很巧妙的一道题，比赛时很多人写的$O(nlogn)$方法模拟。但最优解可以到$O(n)$，这里借鉴了题解区大佬的思路，写一下自己的理解。

题目描述很简练，给定一个数组，我们对数组只有一种操作：每次将比前面紧挨着的数小的数删掉。问题是经过多少次操作能终止（即形成一个非降序序列）。不妨将每个数被删除的时刻记为$t$，问题则转换成求所有$t$里面的最大值。特别地，存在某些数从头到尾没有被删掉，那么它们地删除时刻应该为0。

继续观察，发现每个数最终都会被前面比它大（不一定紧挨着）的数删掉。但是存在一个问题：假设当前的数是$a$，它前面离它最近的比它大的数为$b$，在删掉$a$之前，$b$是否已经被其他数删掉了？答案是存在，但不影响结果。这里不影响结果指的是，即使$b$被删掉了，$a$被删除的时刻仍然不改变，因为会有另外一个数代替$b$来执行删$a$的操作。既然不影响结果，那我们可以直接把删除$a$的对象固定为$b$，即离$a$最近的比$a$大的数。这样进行等效替换可以比较方便地求出边界。

总结一下，对于每个数$a$，会被它前面离它最近的比它大的数$b$删除，$b$可以通过维护单调栈求得。现在的问题是：如何求$a$的删除时刻？从$b$到$a$中间的数应该都小于$a, b$，它们的删除时刻应该比$a$早（因为如果不把这些数删掉，根据题意，$b$和$a$中间只要隔着其他数，就不能执行删除操作）。因此，算出这些数的操作时刻的最大值（记为$m_t$），则$m_t+1$即为$a$的删除时刻。

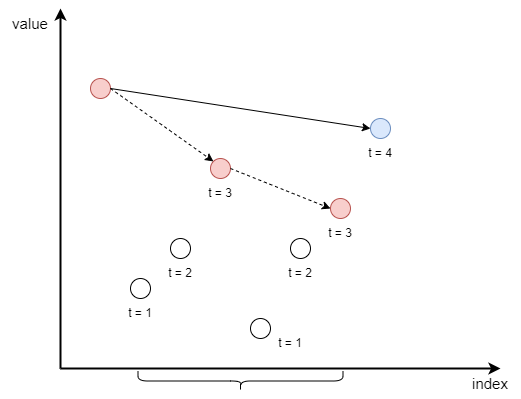
现在问题变成了：如何求$b$到$a$之间的数的删除时刻最大值？区间最值问题可以利用线段树来维护，但是有更巧妙的做法，也是本题的精髓所在。我们不妨将$b$到$a$之间的数看成若干段连续的单调递增序列（参考下面的示意图），每个单调增序列里面的元素的删除时刻也是单增的。因此，当我们考虑蓝色点$a$的删除时刻时，只需要求区间内红色点的最大值+1即可。但如何维护这些红色点的最大值呢？如果一个红色点$R$比它之前的红色点$r$大，那么对于后面的红色点来说，$r$永远都不可能为最大值了。因此可以把$r$删掉，同时这也就形成了一个单调递减栈。因此对于蓝色点来说，我们可以比较一下它跟栈顶的红色点的大小，对于比它小的红色点，直接弹出，直到遇到比自己大的红色点，或者栈空为止。

T3

Code Q3
class Solution {
public:
    int totalSteps(vector<int>& nums) {
        stack<pair<int, int>> stk;
        int res = 0;
        for (int x : nums) {
            int ma = 0;
            while (stk.size() && stk.top().first <= x) {
                ma = max(ma, stk.top().second);
                stk.pop();
            }
            if (stk.size()) ma ++;
            res = max(res, ma);
            stk.push({x, ma});
        }
        return res;
    }
};

到达角落需要移除障碍物的最小数目

一道裸的01 BFS题目。当图里面的边权只有0和1时，可以采用01 BFS来做。这里将有障碍物的格子视为代价为1的边，没有障碍物的格子视为代价为0的边。和朴素BFS不同的是，01 BFS在添加代价为0的边到队列中时，是在队头插入，原因是BFS是逐层搜索，而当搜到代价为0的边时，也应该在当前层被遍历到，对于任意时刻的队列，都满足二段性，即队头开始的连续一段是当前层，之后一段是下一层，而01 BFS就是巧妙地将代价为0的点插入到当前层（即插在队头处）。

Code Q4
class Solution {
public:
    int minimumObstacles(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<int>> dist(n, vector<int>(m, -1));

        deque<pair<int, int>> dq;
        dq.push_back({0, 0});
        dist[0][0] = grid[0][0] == 0 ? 0 : 1;

        int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

        while (dq.size()) {
            auto top = dq.front(); dq.pop_front();
            for (int i = 0; i < 4; i++) {
                int a = top.first + dx[i], b = top.second + dy[i];
                if (a >= 0 && a < n && b >= 0 && b < m) {
                    if (dist[a][b] != -1) continue;
                    if (grid[a][b] == 0) {
                        dist[a][b] = dist[top.first][top.second];
                        dq.push_front({a, b});
                    } else {
                        dist[a][b] = dist[top.first][top.second] + 1;
                        dq.push_back({a, b});
                    }
                }
            }
        }
        return dist[n - 1][m - 1];
    }
};