LC

Motivation

本贴主要用于收录（包括但不限于LeetCode周赛，ACWing周赛）个人觉得比较好做不出来的题，之后的周赛题解都会更新在这个贴子下面，不再开新帖了（不然我的blog里面全都是题解(ಥ _ ಥ))。

Content

Solution

本题比较棘手的地方在于需要满足不能跟别的乘客同时到达，可以利用哈希表记录所有乘客的到达时间，并判断是否重复。注意到上车时刻只能在2种情况中出现：某趟车的到达时刻、某位乘客的到达时刻-1。

class Solution {
public:
    int latestTimeCatchTheBus(vector<int>& b, vector<int>& p, int cap) {
        sort(b.begin(), b.end());
        sort(p.begin(), p.end());

        unordered_set<int> S;
        for (int x : p) S.insert(x);

        int res = 0;
        for (int i = 0, j = 0; i < b.size(); i++) {
            int s = 0;
            while (j < p.size() && p[j] <= b[i] && s < cap) {
                if (!S.count(p[j] - 1)) res = p[j] - 1;
                j++, s++;
            }
            if (s < cap && !S.count(b[i])) res = b[i];
        }
        return res;
    }
};

要使得差值平方和最小，一个直观的想法是尽量让差值绝对值较大的pair变小，这样操作后对平方和的贡献是最大的（所谓贡献，即是平方和的下降幅度），不难证明这种贪心策略是正确的。本题转换为：给定一组数和一个操作数$k$，每次操作将最大元素的值减一，求操作$k$次之后的数组。由于$k$很大，直接模拟必然超时，我们可以观察其中的数学规律。不妨将数组从大到小排序，当我们将最大元素（记为$d_1$）降为次大元素（记为$d_2$）时，需要用掉$d_1 - d_2$个操作；此时会得到2个最大元素，将这2个最大元素降为次大元素时，需要用掉$2\times(d_2 - d_3)$个操作。不难发现，在将第$i$行降到第$i+1$行时，需要$i\times(d_i - d_{i+1})$个操作。参考下图，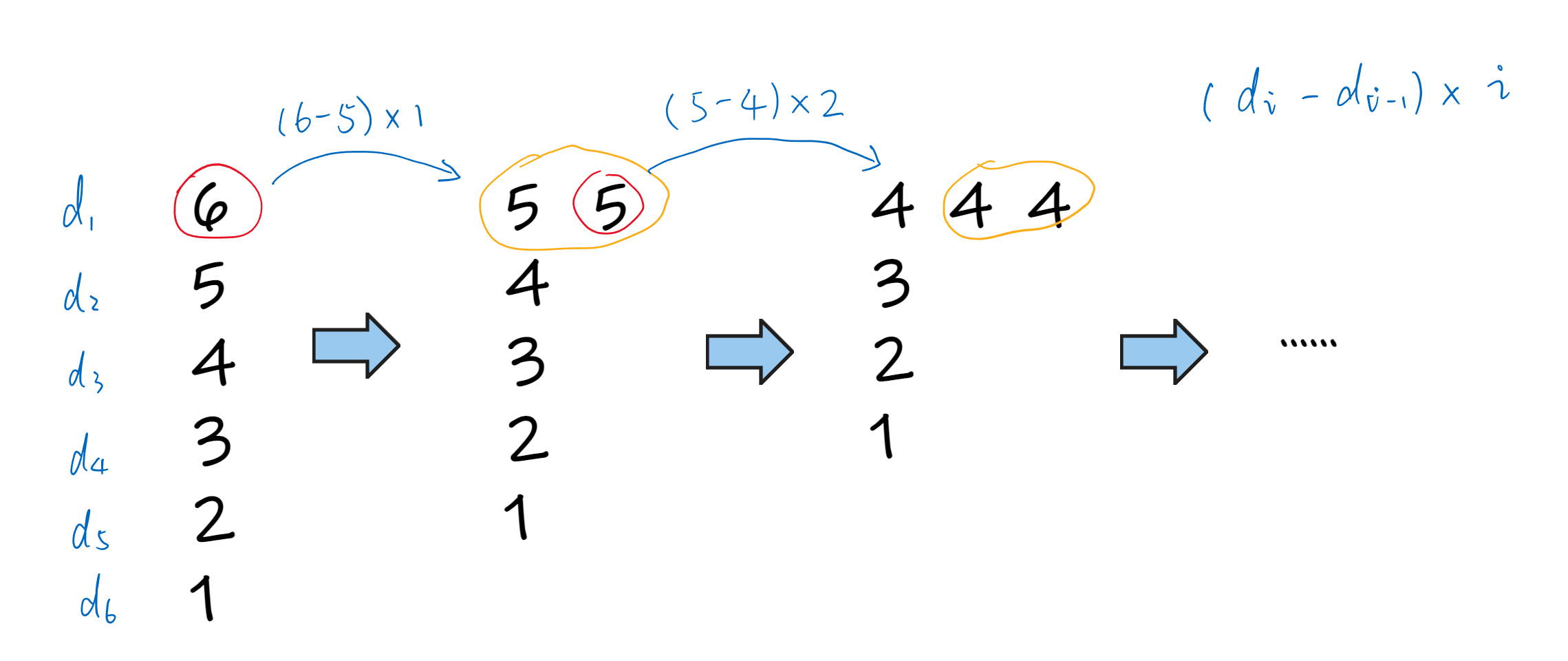
LC

class Solution {
public:
    long long minSumSquareDiff(vector<int>& nums1, vector<int>& nums2, int k1, int k2) {
        vector<int> d;
        for (int i = 0; i < nums1.size(); i++) 
            d.push_back(abs(nums1[i] - nums2[i]));
        sort(d.begin(), d.end(), [&](int a, int b){
            return a > b;
        });
        
        d.push_back(0);
        
        int k = k1 + k2;
        long long s = 0;
   
        for (int i = 0, j = 1; i + 1 < d.size(); i++, j++) {
            s += (d[i] - d[i + 1]) * (long long)j;
            if (s > k) {       
                int q = (s - k) / (i + 1);  // 对于前i个数，每个数需要补回多少
                int r = (s - k) % (i + 1);  // 前i个数补回之后仍有余量，补到数组前面

                for (int w = 0; w < r; w ++) 
                    d[w] = d[i + 1] + q + 1;
                
                for (int w = r; w <= i; w ++) 
                    d[w] = d[i + 1] + q;
                
                break;
            }
        }
        if (s <= k) return 0; 
        
        long long res = 0;
        for (int i = 0; i < d.size(); i++) {
            res += (long long)d[i] * d[i];
        }
        
        return res;
    }
};

用并查集维护连续的一段区间，并记录区间长度，当长度达到$k$时说明找到答案。这里用到了并查集区间染色的技巧，即每次标记一个元素时，将其与右边元素合并，从而构成一条链，这条链表示一段已经标记的区间。

class Solution {
public:

    vector<int> p, s, id;

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    int validSubarraySize(vector<int>& nums, int threshold) {
        int n = nums.size();
        p = s = id = vector<int> (n + 1);
        for (int i = 0; i <= n; i++) {
            p[i] = id[i] = i;
            s[i] = 1;
        }

        id.pop_back();
        sort(id.begin(), id.end(), [&](int a, int b) {
            return nums[a] > nums[b];
        });

        for (int k = 1, i = 0; k <= n; k++) {
            while (i < n && nums[id[i]] > threshold / k) {
                int a = id[i], b = find(id[i] + 1);
                s[b] += s[a];
                if (s[b] - 1 >= k) return k;  // 这里减一是因为区间长度要除去并查集的根节点
                p[a] = b;
                i++;
            }
        }
        return -1;
    }
};

如果理想数组中的元素互不相同，那么该数组的最大长度也是比较小的（$log_210^4\approx14$）。因此我们可以暴搜/记忆化搜索得到所有的方案。这里我们采用动态规划的方式，记$f(i,j)$为数组最大值为$i$且长度为$j$的元素互不相同的理想数组的数量。那么由$f(i,j)$可以得到$f(i\times k, j + 1)$。

第二步是将长度为$j$的元素互不相同的理想数组扩展为长度为$n$的元素可以相同的理想数组。这可以抽象为一个不定方程系数分配问题，即已知$a_1x_1 + a_2x_2 + … + a_jx_j$，且$a_1 + a_2 + … + a_j = n$，求$a_1, a_2, …, a_j$的组合数。可以采用排列组合中的隔板法来解决，答案为：$C_{n-1}^{j-1}$。

class Solution {
public:
    int idealArrays(int n, int ma) {
        const int MOD = 1e9 + 7;
        vector<vector<int>> f(ma + 1, vector<int>(15));
        for (int i = 1; i <= ma; i++) f[i][1] = 1;
        for (int j = 1; j < 14; j++) {
            for (int i = 1; i <= ma; i++) {
                for (int k = 2; k * i <= ma; k++) {
                    f[k * i][j + 1] = (f[k * i][j + 1] + f[i][j]) % MOD;
                }
            }
        }

        vector<vector<int>> C(n + 1, vector<int>(15));
        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= 14 && j <= i; j++) {
                if (!j) C[i][j] = 1;
                else C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % MOD;
            }
        }
        
        int res = 0;
        for (int i = 1; i <= ma; i++) {
            for (int j = 1; j <= 14 && j <= n; j++) {
                res = (res + (long long)f[i][j] * C[n - 1][j - 1]) % MOD;
            }
        }
        return res;
    }
};

求连通分量可以用并查集来维护，本题的主要难点在于如何判环。根据题意，环指的是简单环，它的充要条件是图中每个结点的度为2，因此在求完连通分量后再依次判断一下每个连通分量是否为环即可，如果一个结点的度不等于2，那么它所在的连通分量不为环。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 200010;

int p[N], d[N];
bool st[N];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    int n, m;
    cin >> n >> m;
    
    for (int i = 1; i <= n; i++) p[i] = i;
    
    while (m -- ) {
        int a, b;
        cin >> a >> b;
        p[find(a)] = find(b);
        d[a]++, d[b]++;
    }
    
    for (int i = 1; i <= n; i++) {
        if (d[i] != 2)
            st[find(i)] = true;
    }
    
    int res = 0;
    for (int i = 1; i <= n; i++) {
        if (!st[i] && p[i] == i) res++;
    }
    
    cout << res << endl;
    
    
    return 0;
}